The following is a nonexhaustive list of research directions that emerged during the collaboration among the partners of the OptHySYS project.
Equilibria of linear systems feedbacks with a play operator
 OptHySYS Contributors: Matteo Cocetti, Luca Zaccarian, Fabio Bagagiolo, Enrico Bertolazzi
OptHySYS Contributors: Matteo Cocetti, Luca Zaccarian, Fabio Bagagiolo, Enrico Bertolazzi
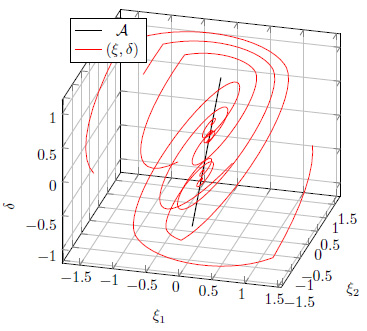
Description: We consider the feedback interconnection of a strictly proper single input single output plant with a play (equivalently backlash) operator. Under the standard assumption that the linear feedback is exponentially stable, so that they play effect is seen as an undesired perturbation, we characterize the set of equilibria of the arising nonlinear closed-loop system and show that it is a bounded set containing the origin. Then we provide necessary and sufficient conditions for global exponential stability of this set, that correspond to exponential stability of the open-loop dynamics. We prove our main result by proposing a novel model for the play operator, corresponding to a constrained differential inclusion, for which we provide extensive comparison with existing models, in terms of the ensuing solutions. With this representation, we also show that the nonlinear closed loop under consideration can be projected to a subspace where it evolves like a switching linear system whose exponential stability implies global asymptotic stability of the (compact) set of equilibria of the original nonlinear dynamics. We illustrate our results by some numerical simulations illustrating the various possible scenarios.
References:
[1] M. Cocetti, L. Zaccarian, F. Bagagiolo, E. Bertolazzi Necessary and sufficient stability conditions for equilibria of linear SISO feedbacks with a play operator". In 10th IFAC Symposium on Nonlinear Control Systems, (NOLCOS 2016).
Stability of hybrid limit cycles
 OptHySYS Contributors: Andrea Bisoffi, Luca Zaccarian
OptHySYS Contributors: Andrea Bisoffi, Luca Zaccarian
External collaborators: Fulvio Forni (University of Cambridge, UK)
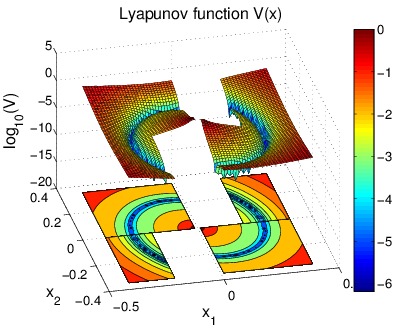
Description: We study the existence of asymptotically stable periodic trajectories induced by reset feedback. Casting the problem into the hybrid setting, we show that a periodic orbit arises from the balance between the energy dissipated during flows and the energy restored by resets, at jumps. The stability of the periodic orbit can be studied with hybrid Lyapunov functions such as the one shown in the figure. The satisfaction of the basic hybrid conditions ensures the robustness of stability of the periodic orbit. A long term goal of this research is the study of control systems that may switch among a set of asymptotically stable orbits according to some optimality criterion. Such an optimization may be also performed through some form of hybrid adaptation. Various application can be envisioned from this study, including running robots, hopping robots and control of mechanical systems subject to impacts.
References:
[1] A. Bisoffi, F. Forni, M. Da Lio and L. Zaccarian. "Global results on reset-induced periodic trajectories of planar systems". Submitted to the 2016 European Control Cofnerence. Aalborg (DK), July 2016.
Semi-Analytical Minimum Time Solutions for Vehicle Trajectory Following
OptHySYS Contributors: Marco Frego, Enrico Bertolazzi, Daniele Fontanelli, Luigi Palopoli
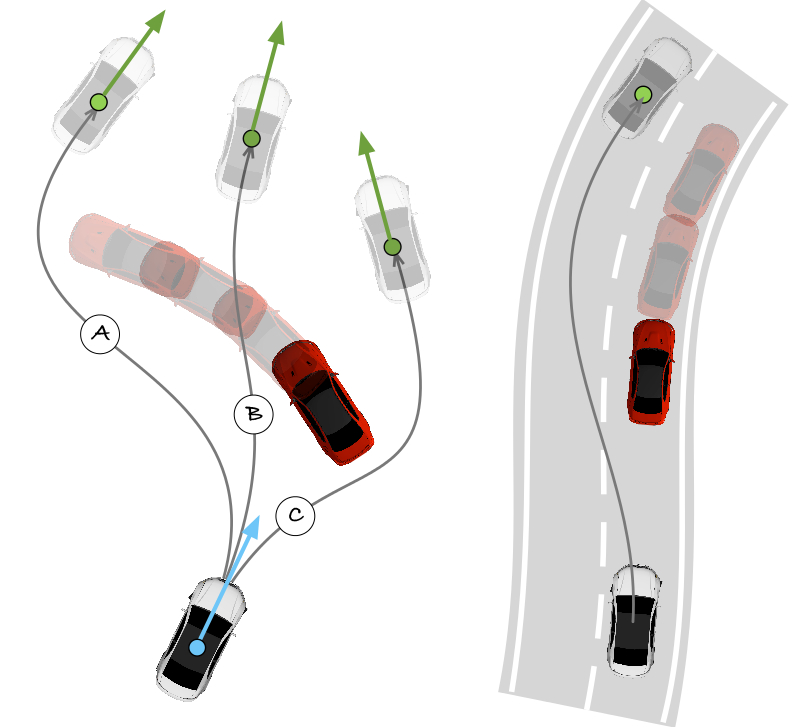
Description: We show a semi-analytical solution to the minimum time optimal control for a vehicle between two given configurations. The vehicle is assumed to follow a clothoid. However, our approach can be generalised to any smooth trajectory. Our technique explicitly considers non–linear dynamics and aerodynamic drag effect, control bounds and acceleration and speed constraints, which leads to a Riccati differential equation. The semi-analytical solution presented here does not need a numerical forward and backward integration as in other works, but it uses pure analytical speed profiles to numerically find the switching points.
References:
[2] M. Frego, E. Bertolazzi, F. Biral, D. Fontanelli and L. Palopoli. "Semi-Analytical Minimum Time Solutions for a Vehicle Following Clothoid-Based Trajectory Subject to Velocity Constraints". Submitted to the 2016 European Control Cofnerence. Aalborg (DK), July 2016.
Optimal Control on Multi-Domains and Hybrid Thermostatic Approximation
 OptHySYS Contributors: Fabio Bagagiolo, Rosario Maggistro.
OptHySYS Contributors: Fabio Bagagiolo, Rosario Maggistro.
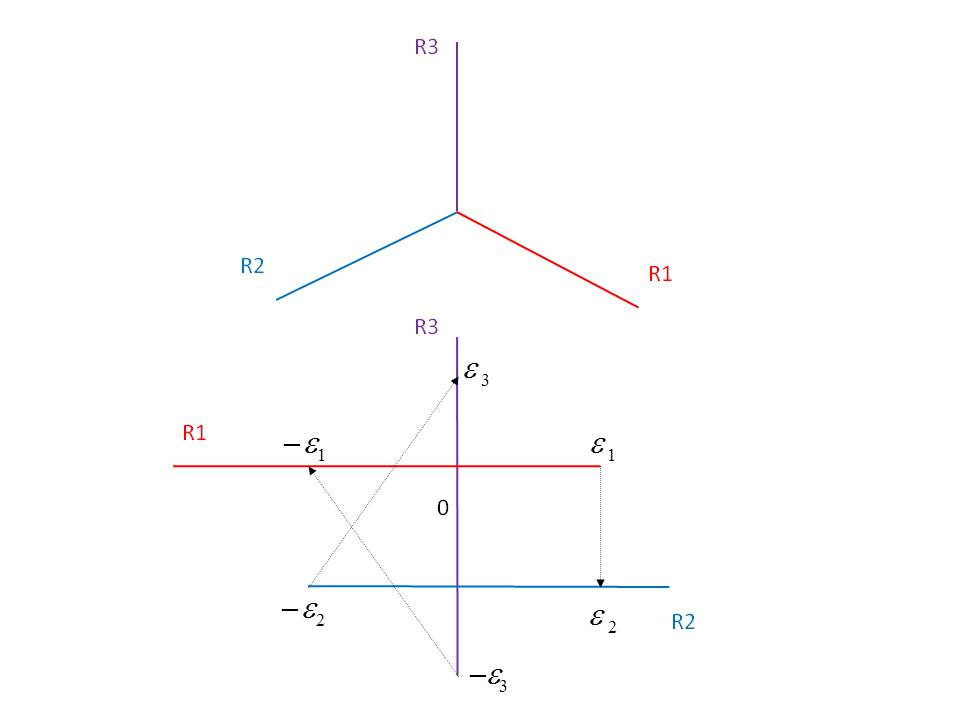
Description: We are investigating the dynamic programming method and the corresponding Hamilton-Jacobi equation for optimal control problems where the controlled dynamics are subject to discontinuity when crossing some fixed hypersurfaces. The corresponding Hamilton-Jacobi equation is then discontinuous and needs a suitable interpretation. Our approach is to approximate the discontinuity by a so-called delayed thermostat which can be also seen as a model of hybrid system. We study the limiting procedure when the thresholds distance of the delayed thermostat goes to zero, and so collapsing to the intial discontinuous situation. We also apply this method to optimal control on networks.
References:
[1] F. Bagagiolo, R. Maggistro: "Thermostatic Approximation of Optimal control Problems on Multi-Domains". In preparation. Already presented at the conferences: 13th Viennese Workshop on Optimal Control Wien 2015, and SIAM Conference on Control and its Applcations Paris 2015.

